Random Variables

ns-3 contains a built-in pseudo-random number generator (PRNG). It is important for serious users of the simulator to understand the functionality, configuration, and usage of this PRNG, and to decide whether it is sufficient for his or her research use.

Quick Overview

ns-3 random numbers are provided via instances of ns3::RandomVariable.

• by default, ns-3 simulations use a fixed seed; if there is any randomness in the simulation, each run of the program will yield identical results unless the seed and/or run number is changed.
• in ns-3.3 and earlier, ns-3 simulations used a random seed by default; this marks a change in policy starting with ns-3.4.
• to obtain randomness across multiple simulation runs, you must either set the seed differently or set the run number differently. To set a seed, call ns3::SeedManager::SetSeed() at the beginning of the program; to set a run number with the same seed, call ns3::SeedManager::SetRun() at the beginning of the program; see Seeding and independent replications.
• each RandomVariable used in ns-3 has a virtual random number generator associated with it; all random variables use either a fixed or random seed based on the use of the global seed (previous bullet);
• if you intend to perform multiple runs of the same scenario, with different random numbers, please be sure to read the section on how to perform independent replications: Seeding and independent replications.

Read further for more explanation about the random number facility for ns-3.

Background

Simulations use a lot of random numbers; one study found that most network simulations spend as much as 50% of the CPU generating random numbers. Simulation users need to be concerned with the quality of the (pseudo) random numbers and the independence between different streams of random numbers.

Users need to be concerned with a few issues, such as:

• the seeding of the random number generator and whether a simulation outcome is deterministic or not,
• how to acquire different streams of random numbers that are independent from one another, and
• how long it takes for streams to cycle

We will introduce a few terms here: a RNG provides a long sequence of (pseudo) random numbers. The length of this sequence is called the cycle length or period, after which the RNG will repeat itself. This sequence can be partitioned into disjoint streams. A stream of a RNG is a contiguous subset or block of the RNG sequence. For instance, if the RNG period is of length N, and two streams are provided from this RNG, then the first stream might use the first N/2 values and the second stream might produce the second N/2 values. An important property here is that the two streams are uncorrelated. Likewise, each stream can be partitioned disjointedly to a number of uncorrelated substreams. The underlying RNG hopefully produces a pseudo-random sequence of numbers with a very long cycle length, and partitions this into streams and substreams in an efficient manner.

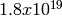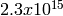ns-3 uses the same underlying random number generator as does ns-2: the MRG32k3a generator from Pierre L’Ecuyer. A detailed description can be found in http://www.iro.umontreal.ca/~lecuyer/myftp/papers/streams00.pdf. The MRG32k3a generator provides independent streams of random numbers, each of which consists of substreams. Each substream has a period (i.e., the number of random numbers before overlap) of 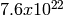. The period of the entire generator is .

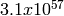Class ns3::RandomVariable is the public interface to this underlying random number generator. When users create new RandomVariables (such as ns3::UniformVariable, ns3::ExponentialVariable, etc.), they create an object that uses one of the distinct, independent streams of the random number generator. Therefore, each object of type ns3::RandomVariable has, conceptually, its own “virtual” RNG. Furthermore, each ns3::RandomVariable can be configured to use one of the set of substreams drawn from the main stream.

An alternate implementation would be to allow each RandomVariable to have its own (differently seeded) RNG. However, we cannot guarantee as strongly that the different sequences would be uncorrelated in such a case; hence, we prefer to use a single RNG and streams and substreams from it.

Seeding and independent replications

ns-3 simulations can be configured to produce deterministic or random results. If the ns-3 simulation is configured to use a fixed, deterministic seed with the same run number, it should give the same output each time it is run.

By default, ns-3 simulations use a fixed seed and run number. These values are stored in two ns3::GlobalValue instances: g_rngSeed and g_rngRun.

A typical use case is to run a simulation as a sequence of independent trials, so as to compute statistics on a large number of independent runs. The user can either change the global seed and rerun the simulation, or can advance the substream state of the RNG, which is referred to as incrementing the run number.

A class ns3::SeedManager provides an API to control the seeding and run number behavior. This seeding and substream state setting must be called before any random variables are created; e.g:

SeedManager::SetSeed (3);  // Changes seed from default of 1 to 3
SeedManager::SetRun (7);  // Changes run number from default of 1 to 7
// Now, create random variables
UniformVariable x(0,10);
ExponentialVariable y(2902);
...

Which is better, setting a new seed or advancing the substream state? There is no guarantee that the streams produced by two random seeds will not overlap. The only way to guarantee that two streams do not overlap is to use the substream capability provided by the RNG implementation. Therefore, use the substream capability to produce multiple independent runs of the same simulation. In other words, the more statistically rigorous way to configure multiple independent replications is to use a fixed seed and to advance the run number. This implementation allows for a maximum of 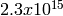independent replications using the substreams.

For ease of use, it is not necessary to control the seed and run number from within the program; the user can set the NS_GLOBAL_VALUE environment variable as follows:

NS_GLOBAL_VALUE="RngRun=3" ./waf --run program-name

Another way to control this is by passing a command-line argument; since this is an ns-3 GlobalValue instance, it is equivalently done such as follows:

./waf --command-template="%s --RngRun=3" --run program-name

or, if you are running programs directly outside of waf:

./build/optimized/scratch/program-name --RngRun=3

The above command-line variants make it easy to run lots of different runs from a shell script by just passing a different RngRun index.

Class RandomVariable

All random variables should derive from class RandomVariable. This base class provides a few static methods for globally configuring the behavior of the random number generator. Derived classes provide API for drawing random variates from the particular distribution being supported.

Each RandomVariable created in the simulation is given a generator that is a new RNGStream from the underlying PRNG. Used in this manner, the L’Ecuyer implementation allows for a maximum of 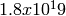random variables. Each random variable in a single replication can produce up to 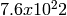random numbers before overlapping.

Base class public API

Below are excerpted a few public methods of class RandomVariable that access the next value in the substream.:

/**
 * \brief Returns a random double from the underlying distribution
 * \return A floating point random value
 */
double GetValue (void) const;

/**
 * \brief Returns a random integer integer from the underlying distribution
 * \return  Integer cast of ::GetValue()
 */
uint32_t GetInteger (void) const;

We have already described the seeding configuration above. Different RandomVariable subclasses may have additional API.

Types of RandomVariables

The following types of random variables are provided, and are documented in the ns-3 Doxygen or by reading src/core/random-variable.h. Users can also create their own custom random variables by deriving from class RandomVariable.

• class UniformVariable
• class ConstantVariable
• class SequentialVariable
• class ExponentialVariable
• class ParetoVariable
• class WeibullVariable
• class NormalVariable
• class EmpiricalVariable
• class IntEmpiricalVariable
• class DeterministicVariable
• class LogNormalVariable
• class TriangularVariable
• class GammaVariable
• class ErlangVariable
• class ZipfVariable

Semantics of RandomVariable objects

RandomVariable objects have value semantics. This means that they can be passed by value to functions. The can also be passed by reference to const. RandomVariables do not derive from ns3::Object and we do not use smart pointers to manage them; they are either allocated on the stack or else users explicitly manage any heap-allocated RandomVariables.

RandomVariable objects can also be used in ns-3 attributes, which means that values can be set for them through the ns-3 attribute system. An example is in the propagation models for WifiNetDevice::

TypeId
RandomPropagationDelayModel::GetTypeId (void)
{
  static TypeId tid = TypeId ("ns3::RandomPropagationDelayModel")
    .SetParent<PropagationDelayModel> ()
    .AddConstructor<RandomPropagationDelayModel> ()
    .AddAttribute ("Variable",
                   "The random variable which generates random delays (s).",
                   RandomVariableValue (UniformVariable (0.0, 1.0)),
         MakeRandomVariableAccessor (&RandomPropagationDelayModel::m_variable),
                   MakeRandomVariableChecker ())
    ;
  return tid;
}

Here, the ns-3 user can change the default random variable for this delay model (which is a UniformVariable ranging from 0 to 1) through the attribute system.

Using other PRNG

There is presently no support for substituting a different underlying random number generator (e.g., the GNU Scientific Library or the Akaroa package). Patches are welcome.

More advanced usage

To be completed.

Publishing your results

When you publish simulation results, a key piece of configuration information that you should always state is how you used the the random number generator.

• what seeds you used,
• what RNG you used if not the default,
• how were independent runs performed,
• for large simulations, how did you check that you did not cycle.

It is incumbent on the researcher publishing results to include enough information to allow others to reproduce his or her results. It is also incumbent on the researcher to convince oneself that the random numbers used were statistically valid, and to state in the paper why such confidence is assumed.

Summary

Let’s review what things you should do when creating a simulation.

• Decide whether you are running with a fixed seed or random seed; a fixed seed is the default,
• Decide how you are going to manage independent replications, if applicable,
• Convince yourself that you are not drawing more random values than the cycle length, if you are running a very long simulation, and
• When you publish, follow the guidelines above about documenting your use of the random number generator.