App Store Technical Requirements
Main Page - Roadmap - Summer Projects - Project Ideas - Developer FAQ - Tools - Related Projects
HOWTOs - Installation - Troubleshooting - User FAQ - Samples - Models - Education - Contributed Code - Papers
Goals
The long-term goal is to move ns-3 to separate modules, for build and maintenance reasons. For build reasons, since ns-3 is becoming large, we would like to allow users to enable/disable subsets of the available model library. For maintenance reasons, it is important that we move to a development model where modules can evolve on different timescales and be maintained by different organizations.
An analogy is the GNOME desktop, which is composed of a number of individual libraries that evolve on their own timescales. A build framework called jhbuild exists for building and managing the dependencies between these disparate projects.
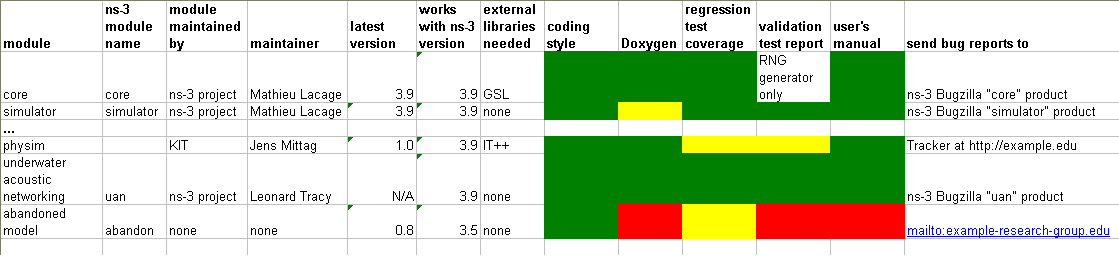
Once we have a modular build, and an ability to separately download and install third-party modules, we will need to distinguish the maintenance status or certification of modules. The ns-3 project will maintain a set of core ns-3 modules including those essential for all ns-3 simulations, and will maintain a master build file containing metadata to contributed modules; this will allow users to fetch and build what they need. Eventually, modules will have a maintenance state associated with them describing aspects such as who is the maintainer, whether it is actively maintained, whether it contains documentation or tests, whether it passed an ns-3 project code review, whether it is currently passing the tests, etc. The current status of all known ns-3 modules will be maintained in a database and be browsable on the project web site.
Figure caption: Mock-up of future model status page (models and colors selected are just for example purposes)
The basic idea of the ns-3 app store would be to store on a server a set of user-submitted metadata which describes various source code packages. Typical metadata would include:
- unique name
- version number
- last known good ns-3 version (tested against)
- description
- download url
- untar/unzip command
- configure command
- build command
- system prerequisites (if user needs to apt-get install other libraries)
- list of ns-3 package dependencies (other ns-3 packages which this package depends upon)
Requirements
Build and configuration
- Enable optimized, debug, and static builds
- Separate tests from models
- Doxygen support
- Test.py framework supports the modularization
- Python bindings support the modularization
- integrate lcov code coverage tests
- integrate with buildbots
API and work flow
Assume that our download script is called download.py and our build script is called build.py.
wget http://www.nsnam.org/releases/ns-allinone-3.x.tar.bz2 bunzip2 ns-allinone-3.x.tar.bz2 && tar xvf ns-allinone-3.x.tar.bz2 cd ns-allinone-3.x
In this directory, users will find the following directory layout:
build.py download.py constants.py? VERSION LICENSE README
Download essential modules:
./download.py
This will leave a layout such as follows:
download.py build.py pygccxml pybindgen simulator core common gcc-xml
For typical users, the next step is as follows:
./build.py ns3
"ns3" is a meta-module that pulls in what constitutes what is considered to be the core of an ns-3 release (i.e. for starters, every module that is in ns-3.9).
The above will take the following steps:
- build all typical prerequisites such as pybindgen
- cd core
- ./waf configure && ./waf && ./waf install
The above will install headers into build/debug/ns3/ and a libns3core.so into build/debug/lib/
cd ../simulator ./waf configure && ./waf && ./waf install cd .. ...
Open issue: What granularity of modules should we maintain? Continue with core, simulator, common, node? Merge them somehow?
Open issue: How to express and honor platform limitations, such as only trying to download/build NSC on platforms supporting it.
Once the build process is done, there will be a bunch of libraries in a common build directory, and all applicable headers. Specifically, we envision for module foo, there may be a libns3foo.so, libns3foo-test.so, a python .so, and possibly others.
Python
We have a few choices for supporting Python. First, note that this type of system provides an opportunity for the python build tools to be added as packages to the overall build system, so that users can more easily build their bindings. We can try to build lots of small python modules, or run a scan at the very end of the ns-3 build process to build a customized python ns3 module, such as:
- python-scan.py
- ...
- pybindgen
which operates on the headers in the build/debug/ns3 directory and creates a python module .so library that matches the ns-3 configured components.
Open issue: What is the eventual python API? Should each module be imported separately such as import node as ns.node, or should we try to go for a single ns3 python module?
Or, we could continue to maintain bindings. Another consideration is that constantly generating bindings will slow down the builds.
Tests
Tests are run by running ./test.py, which knows how to find the available test libraries and run the tests.
Presently, test.py hardcodes the examples or samples; it needs to become smarter to learn what examples are around and need testing.
Doxygen
Doxygen can be run such as "build.py doxygen" on the build/debug/ns3 directory. I would guess that we don't try to modularize this but instead to run on the build/debug/ns3/ directory once all headers have been copied in.
Build flags
To configure different options such as -g, -fprofile-arcs, e.g., use the CFLAGS environment variable.
Running programs
To run programs:
./build.py shell build/debug/examples/csma/csma-bridge
or
python build/debug/examples/csma/csma-bridge.py
Other examples
Build all known ns-3 modules:
./build.py all
In the above case, suppose that the program could not download and fetch a module. Here, it can interactively prompt the user "Module foo not found; do you wish to continue [Y/n]?".
Build the core of ns-3, plus device models WiFi and CSMA:
./build ns3-core wifi csma
ns3-core is a meta-module containing simulator core common node. Open issue: what is the right granularity for this module?
Suppose a research group at Example Univ. publishes a new WiMin device module. It gets a new unique module name from ns-3 project, such as wimin. It also contributes metadata to the master ns-3 build script. When a third-party does the following:
./build.py wimin
the system will try to download and build the new wimin module (plus its examples and tests), and put it in the usual place.
Plan
GNOME jhbuild seems to be able to provide most or all of the "build.py" and "download.py" functionality mentioned above. jhbuild may need to be wrapped by a specialized ns-3 build.py or download.py wrapper. So, the current plan is to try to prototype the above using jhbuild and se how far we get
Work can proceed in parallel:
- Start to try to compare jhbuild with our existing download.py/build.py at the top level directory
- Try to define the module granularity and fix broken module dependencies
- Work on python bindings
- Work on how to handle examples in a modular test framework