HOWTO get ns-3 to detect steady-state times in your data: Difference between revisions
No edit summary |
No edit summary |
||
| Line 113: | Line 113: | ||
== Algorithms Currently Trying == | == Algorithms Currently Trying == | ||
* Batch Means Test | |||
** '''White, K., Cobb, M., & Spratt, S. (2000)'''. A Comparison of Five Steady-state Truncation Heuristics for Simulation. ''Proceedings of the 32nd Winter Simulation Conference (WSC '00)'', 755–760. | |||
*** In this reference, they say: "Cash, et al. (1992), Nelson (1992), and Goldsman, et al. (1994), propose a family of related tests for detecting the presence of bias in an output series. These tests generalize and extend the earlier work Schruben (1982) and Schruben, et al. (1983)." | |||
** Algorithm: Bias detection test. | |||
** Reason: Steady-state detection method can detect if not in steady-state (unlike MSER-5). | |||
** Reason: Single-replicate algorithm. | |||
== Algorithms to Try (In order that they should be tried) == | == Algorithms to Try (In order that they should be tried) == | ||
Revision as of 18:17, 25 July 2011
Framework
Steady-state detectors
The architecture of SAFE provides for the use of mechanisms to determine when metrics estimated through simulation have reached steady-state. Although well known, the initialization bias problem hasn't been addressed satisfactorily in the domain of network simulation. Few published research studies have taken steps to exclude samples generated during model transients from their statistical data analysis. Among other researchers who have identified the relevance of initialization bias in network simulation, "Perrone, Yuan, and Nicol [2003]":http://redmine.eg.bucknell.edu/safe/attachments/16/perrone2003.pdf report the significance of avoiding the use of samples from transient in the computation of statistical estimators for metrics of interest.
SAFE enables one to hook up a source of samples to an analysis module, which determines on its own whether the sample data is "in transient" or in steady-state.
The development of _steady-state detectors_ for SAFE is looking at a broad range of publications that will culminate in the identification of sound data analysis methodology. SAFE will use the information provided by steady-state detectors to implement data deletion in the samples collected thereby avoiding initialization bias.
Current Stage of Development
This work is at an investigation stage. We are currently going through the literature to identify algorithms that will be suitable for use in SAFE steady-state detectors.
Projected Milestones
- Literature search and evaluation: June 8-14, 2011
- First implementation: June 15-30, 2011
- Evaluation of implementation against synthetic data generator: July 1-20, 2011
References to Get
- Law, A. M. (2007). Simulation Modeling and Analysis. 4th ed. New York: McGraw-Hill.
- Algorithm: Batch means for steady-state detection. (See pp. 528–529.)
- Reason: An overview of simulation.
- Reason: An overview of single-replicate techniques.
- Reason: Single-replicate algorithm.
- Anderson, T. W. (1994). The Statistical Analysis of Time Series. New York: Wiley.
- Algorithm: Spectral methods for steady-state detection.
- Reason: Single-replicate algorithm.
- Schruben, L. (1982). Detecting Initialisation Bias in Simulation Output. Operations Research, 30(3), 569-590.
- Algorithm: Standardized time series methods for steady-state detection.
- Reason: Single-replicate algorithm.
- Schruben, L. W. (1983). Confidence Interval Estimation using Standardized Time Series. Operations Research 31:1090–1108.
- Algorithm: Standardized time series methods for confidence intervals.
- Reason: Single-replicate algorithm.
- Schruben, L., Singh, H., and Tierney, L. (1983). Optimal Tests for Initialisation Bias in Simulation Output. Operations Research, 31( 6), 1167-1178.
- Algorithm: Standardized time series methods for steady-state detection.
- Reason: Single-replicate algorithm.
- Nakayama, M. K. (1994). Two-stage Stopping Procedures Based on Standardized Time Series. Management Science 40:1189–1206.
- Algorithm: Standardized time series methods for confidence intervals.
- Reason: Might be a single-replicate algorithm.
- Reason: Confidence interval algorithm.
- Reason: Nakayama presents two-stage procedures for obtaining fixed-width confidence intervals using standardized time series methods.
- Pawlikowski, K., McNickle, D., and Ewing, G. (1998). Coverage of Confidence Intervals from Sequential Steady-state Simulation, Simulation Practice and Theory, 6:255-267.
- Algorithm: Confidence intervals.
- Reason: Confidence interval algorithm.
- Glynn, P. W., and W. Whitt. (1992). The Asymptotic Validity of Sequential Stopping Rules in Stochastic Simulations. Annals of Applied Probability 2:180–198.
- Algorithm: Sequential procedures for confidence intervals.
- Reason: Might be a single-replicate algorithm.
- Reason: Confidence interval algorithm.
- Reason: Glynn and Whitt consider several so-called sequential procedures.
Algorithms Rejected without Trying
- Multiple (3) steady-state algorithms in an Excel based tool.
- Robinson, Stewart (2005). Automated Analysis of Simulation Output Data. Proceedings of the 2005 Winter Simulation Conference.
- Summary: Paper describes an Excel based semi-automated tool that calls SIMUL8.
- Advantages: Automated methods. Describes batch method which works for single seed values.
- Disadvantages: Based on Excel and SIMUL8, which means can't be called from ns-3.
- Note: Has equations for an automated version of Welch's visual method.
- Note: Describes how to automate the batch mean method. See Robinson (2002) in Rejected Algorithms section for equations for batch mean method.
- Note: Describes how to automate the MSER-5 method.
- Schruben's test applied after 25 crossings of the running Mean
- Pawlikowski, K, (1990), Steady State Simulation of Queueing Processes: a Survey of Problems and Solutions, ACM Computing Surveys, 22, June 1990, 123-170.
- McNickle, D., Ewing, G.C., and Pawlikowski, K.. (2007). Transient Deletion And The Quality Of Sequential Steady-State Simulation, Proceedings 21st European Conference on Modelling and Simulation.
- In this reference, they say: "Details of our sequential implementation of a Schruben-based method can be found in Section 3 of Pawlikowski (1990)."
- In this reference, they say that the Akaroa2 simulator requires 25 crossings of the running mean of the values before it performs its Schruben’s test.
- In this reference, they say: "Sequential Spectral Analysis, a modification of the method proposed by Heidelberger and Welch (1981) and specified in Pawlikowski (1990), was used to estimate the confidence interval width. We have found that this method gives accurate confidence intervals, especially for highly correlated data, such as waiting times in highly loaded queues (Ewing, McNickle and Pawlikowski 2002, McNickle, Pawlikowski, and Ewing, 2004).
- Hoad, K., Robinson, S., & Davies, R. (2008). Automating Warm-Up Length Estimation. Proceedings of the 2008 Winter Simulation Conference, 532–540.
- In this reference, they say: "For example, the crossing-of-the-mean rule (Fishman 1973, Wilson and Pritsker 1978a, 1978b) was heavily criticised in the literature for being extremely sensitive to the selection of its main parameter, which was system-dependent, and misspecification of which caused significant over or under-estimation of the warm-up length (Pawlikowski 1990)."
- In this reference, they call Pawlikowski (1990), the "Goodness-Of-Fit method", and they say: "Both the goodness of fit method and Kimbler’s double exponential smoothing method consistently and severely underestimated the truncation point and were therefore rejected."
- Algorithm: Standardized time series methods for steady-state detection.
- Reason: Single-replicate algorithm.
- Statistical Process Control (SPC) Approach
- Robinson, Stewart (2002). A Statistical Process Control Approach for Estimating the Warm-Up Period. Proceedings of the 2002 Winter Simulation Conference.
- Summary: 2 stage method:
- Stage 1: has multiple replications.
- Stage 2: has single seed.
- Advantages: Works with a single seed value for stage 2.
- Disadvantages: Requires visual inspection of final results and initial preliminary runs from Stage 1.
- Note: Has equations for batch mean method, which works for single seeds.
Algorithms Rejected after Trying
- Mean Squared Error Reduction (MSER-5) method applied after 25 crossings of the running Mean
- White, K.P. and Robinson, S. (2010). The Problem of the Initial Transient (Again) or Why MSER Works. Journal of Simulation 4, 268-272.
- Franklin, W.W. and White, K.P. (2008). Stationarity Tests and MSER-5: Exploring the Intuition behind Mean-Squared-Error-Reduction in Detecting and Correcting Initialization Bias. Proceedings of the 2008 Winter Simulation Conference.
- White, K.P. and Cobb, M.J. (2000). A Comparison of Five Steady-State Truncation Heuristics for Simulation. Proceedings of the 2000 Winter Simulation Conference.
- This reference showed that the MSER-5 method performed the best of the five methods tried.
- McNickle, D., Ewing, G.C., and Pawlikowski, K.. (2007). Transient Deletion And The Quality Of Sequential Steady-State Simulation, Proceedings 21st European Conference on Modelling and Simulation.
- In this reference, they say that the Akaroa2 simulator requires 25 crossings of the running mean of the values before it performs its Schruben’s test.
- Summary: MSER-5 tries to reduce the mean squared error.
- Advantages: Single-replicate algorithm.
- Disadvantages:
- Note: The MSER-5 method alone was saying the system was in steady-state with as few as 2 data values.
- Note: My code now requires 25 mean crossings before the MSER-5 method is tried, which means the system is in steady-state and which is the situation the MSER-5 method was intended to work with.
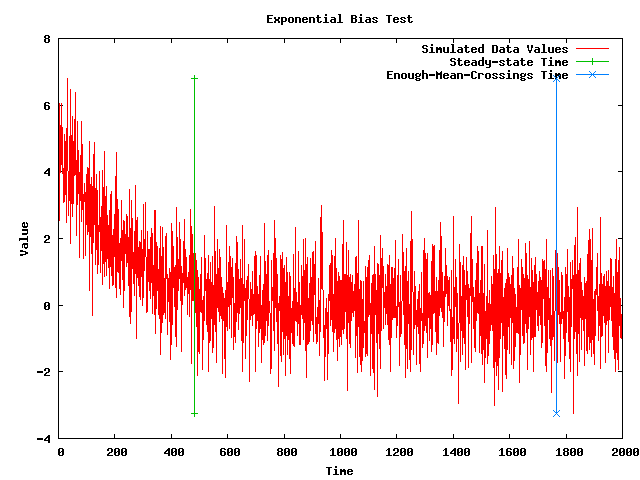
- Note: The following plot shows a simulated data set with an exponential bias along with the steady-state time that my implementation of the MSER-5 algorithm (after 25 mean crossings) is currently returning. The plot also shows vertical lines where the steady-state time is and where the 25th mean crossing takes place.
- Note: My code seems to be giving a better steady-state time than just using the MSER-5 for the first 1,000 points, but it did require almost 2,000 points to get 25 mean crossings.
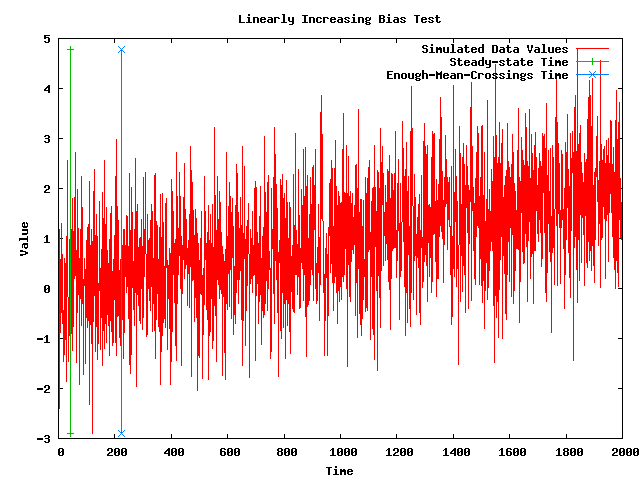
- Note: The following plot shows a simulated data set with a linearly increasing bias along with the steady-state time that my implementation of the MSER-5 algorithm (after 25 mean crossings) is currently returning. The plot also shows vertical lines where the steady-state time is and where the 25th mean crossing takes place.
- Note: The problem with the MSER-5 algorithm is that the data set with a linearly increasing bias in the above plot does NOT have a steady-state time, and so the algorithm should NOT be finding one. So, the MSER-5algorithm is being REJECTED.
- Hoad, K., Robinson, S., & Davies, R. (2008). Automating Warm-Up Length Estimation. Proceedings of the 2008 Winter Simulation Conference, 532–540.
- In this reference, they say: "For example, the crossing-of-the-mean rule (Fishman 1973, Wilson and Pritsker 1978a, 1978b) was heavily criticised in the literature for being extremely sensitive to the selection of its main parameter, which was system-dependent, and misspecification of which caused significant over or under-estimation of the warm-up length (Pawlikowski 1990)."
Algorithms Currently Trying
- Batch Means Test
- White, K., Cobb, M., & Spratt, S. (2000). A Comparison of Five Steady-state Truncation Heuristics for Simulation. Proceedings of the 32nd Winter Simulation Conference (WSC '00), 755–760.
- In this reference, they say: "Cash, et al. (1992), Nelson (1992), and Goldsman, et al. (1994), propose a family of related tests for detecting the presence of bias in an output series. These tests generalize and extend the earlier work Schruben (1982) and Schruben, et al. (1983)."
- Algorithm: Bias detection test.
- Reason: Steady-state detection method can detect if not in steady-state (unlike MSER-5).
- Reason: Single-replicate algorithm.
- White, K., Cobb, M., & Spratt, S. (2000). A Comparison of Five Steady-state Truncation Heuristics for Simulation. Proceedings of the 32nd Winter Simulation Conference (WSC '00), 755–760.
Algorithms to Try (In order that they should be tried)
- Schruben's Maximum Test
- Schruben, L. (1982). Detecting Initialisation Bias in Simulation Output. Operations Research, 30(3), 569-590.
- Summary: Standardized time series methods for steady-state detection.
- Advantages: Single-replicate algorithm.
- Disadvantages:
- Note:
- Schruben's Optimal Test
- Schruben, L., Singh, H., and Tierney, L. (1983). Optimal Tests for Initialisation Bias in Simulation Output. Operations Research, 31( 6), 1167-1178.
- Summary: Standardized time series methods for steady-state detection.
- Advantages: Single-replicate algorithm.
- Disadvantages:
- Note:
- Batch means
- Law, A. M. (2007). Simulation Modeling and Analysis. 4th ed. New York: McGraw-Hill. (See pp. 528–529.)
- Summary: Groups values into batches and computes mean of each batch.
- Advantages:
- Disadvantages:
- Note: