Log-normal Distributed random varLogNormalVariable defines a random variable with log-normal distribution. More...
#include <random-variable.h>
 Inheritance diagram for ns3::LogNormalVariable:
Inheritance diagram for ns3::LogNormalVariable: Collaboration diagram for ns3::LogNormalVariable:
Collaboration diagram for ns3::LogNormalVariable:Public Member Functions | |
| LogNormalVariable (double mu, double sigma) | |
 Public Member Functions inherited from ns3::RandomVariable Public Member Functions inherited from ns3::RandomVariable | |
| RandomVariable () | |
| RandomVariable (const RandomVariable &o) | |
| ~RandomVariable () | |
| uint32_t | GetInteger (void) const |
| Returns a random integer integer from the underlying distribution. More... | |
| double | GetValue (void) const |
| Returns a random double from the underlying distribution. More... | |
| RandomVariable & | operator= (const RandomVariable &o) |
Additional Inherited Members | |
 Protected Member Functions inherited from ns3::RandomVariable Protected Member Functions inherited from ns3::RandomVariable | |
| RandomVariable (const RandomVariableBase &variable) | |
| RandomVariableBase * | Peek (void) const |
Log-normal Distributed random var
LogNormalVariable defines a random variable with log-normal distribution.
If one takes the natural logarithm of random variable following the log-normal distribution, the obtained values follow a normal distribution. This class supports the creation of objects that return random numbers from a fixed lognormal distribution. It also supports the generation of single random numbers from various lognormal distributions.
The probability density function is defined over the interval [0,+inf) as: 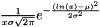 where
where 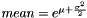 and
and 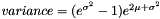
The 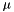 and
and 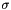 parameters can be calculated if instead the mean and variance are known with the following equations:
parameters can be calculated if instead the mean and variance are known with the following equations: 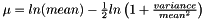 , and,
, and, 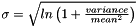
Definition at line 546 of file random-variable.h.
| ns3::LogNormalVariable::LogNormalVariable | ( | double | mu, |
| double | sigma | ||
| ) |
| mu | mu parameter of the lognormal distribution |
| sigma | sigma parameter of the lognormal distribution |
Definition at line 1510 of file random-variable.cc.
References NS_LOG_FUNCTION.